Quick start
When to use it
Parfun works well with tasks that are CPU-intensive and can be easily divided into independent sub-tasks.
Here are a few examples of tasks that can be easily parallelized:
✔ Filtering tasks (e.g.
pandas.Dataframe.filter())✔ Operations that are associative or independent (e.g. matrix addition, sum …)
✔ By-row data processing tasks (e.g. cleaning or normalizing input data).
Not all tasks can be easily parallelized:
✖ Computations on non-partitionable datasets (e.g. median computation, sorting)
✖ I/O intensive tasks (file loading, network communications)
✖ Very short (< 100ms) tasks.
These tasks are too small for the parallelism gains to exceed the overhead of parallelization. Always keep in mind that parallelization is a trade-off between CPU speed and the time needed to transfer data between processes.
Setup and backend selection
First, install the parfun package from PyPI using any compatible package manager:
pip install parfun
The above command will only install the base package. This is suitable for using the multiprocessing backend, however
if you wish to use an alternate computing backend, such as Scaler or Dask, or to enable Pandas’ support,
install the scaler, dask, or pandas extras as required:
pip install "parfun[dask,scaler,pandas]"
Initializing the library
Before using Parfun, the backend must be initialized. This can either be done with set_parallel_backend()
or in a scoped context manager using set_parallel_backend_context().
import parfun as pf
if __name__ == "__main__":
# Set the parallel backend process-wise.
pf.set_parallel_backend("local_multiprocessing")
# Set the parallel backend with a Python context.
with pf.set_parallel_backend_context("scaler_remote", scheduler_address="tcp://scaler.cluster:1243"):
... # Will run the parallel tasks over a remotely setup Scaler cluster.
See set_parallel_backend() for a description of the available backend options.
Your first parallel function
The following example does basic statistical analysis on a stock portfolio. By using Parfun, these metrics are calculated in parallel, splitting the computation by country.
from typing import List
import pandas as pd
import parfun as pf
@pf.parallel(
split=pf.per_argument(portfolio=pf.dataframe.by_group(by="country")),
combine_with=pf.dataframe.concat,
)
def relative_metrics(portfolio: pd.DataFrame, columns: List[str]) -> pd.DataFrame:
"""
Computes relative metrics (difference to mean, median ...) of a dataframe, for each of the requested dataframe's
values, grouped by country.
"""
output = portfolio.copy() # do not modify the input dataframe.
for country in output["country"].unique():
for column in columns:
values = output.loc[output["country"] == country, column]
mean = values.mean()
std = values.std()
output.loc[output["country"] == country, f"{column}_diff_to_mean"] = values - mean
output.loc[output["country"] == country, f"{column}_sq_diff_to_mean"] = (values - mean) ** 2
output.loc[output["country"] == country, f"{column}_relative_to_mean"] = (values - mean) / std
return output
if __name__ == "__main__":
portfolio = pd.DataFrame({
"company": ["Apple", "Citigroup", "ASML", "Volkswagen", "Tencent"],
"industry": ["technology", "banking", "technology", "manufacturing", "manufacturing"],
"country": ["US", "US", "NL", "DE", "CN"],
"market_cap": [2828000000000, 80310000000, 236000000000, 55550000000, 345000000000],
"revenue": [397000000000, 79840000000, 27180000000, 312000000000, 79000000000],
"workforce": [161000, 240000, 39850, 650951, 104503]
})
with pf.set_parallel_backend_context("local_multiprocessing"):
metrics = relative_metrics(portfolio, ["market_cap", "revenue"])
print(metrics)
In this example, the parallel() decorator parallelizes the execution of
relative_metrics() by country, and then reduces the results by concatenating them:
@pf.parallel(
split=pf.per_argument(portfolio=pf.dataframe.by_group(by="country")),
combine_with=pf.dataframe.concat,
)
def relative_metrics(portfolio: pd.DataFrame, columns: List[str]) -> pd.DataFrame:
We tell the parallel engine how to partition the data with the split parameter. Note that we can safely
split the calculation over countries, as the function itself processes these countries independently.
We use
per_argument()to tell the parallel engine which arguments to partition on. In the example, we will only partition on theportfolioargument, and we don’t touch thecolumnsargument.We use
by_group()to specify that the portfolio dataframe can be partitioned over itscountrycolumn.
Finally, Parfun needs to know how to combine the results of the partitioned calls to
relative_metrics(). This is done with the combine_with parameter. In our example, we concatenate the
result dataframes with concat().
Parfun handles executing the function in parallel and collection the results. We can represent this computation visually:
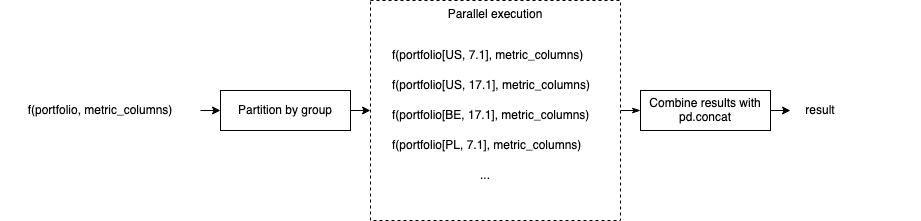
This is a well-known parallelization architecture called map/reduce or scatter/gather.
Partitioning functions
As seen in the example above, the @parallel decorator accepts a partitioning function (split).
Previously, we applied a single partitioning function (by_group()) on a
single argument. However, we can also use per_argument() to apply partitioning
to multiple arguments.
from typing import List
import pandas as pd
import parfun as pf
@pf.parallel(
split=pf.per_argument(
factors=pf.py_list.by_chunk,
dataframe=pf.dataframe.by_row,
),
combine_with=pf.dataframe.concat,
)
def multiply_by_row(factors: List[int], dataframe: pd.DataFrame) -> pd.DataFrame:
assert len(factors) == len(dataframe)
return dataframe.multiply(factors, axis=0)
if __name__ == "__main__":
dataframe = pd.DataFrame({
"A": [1, 2, 3],
"B": [4, 5, 6]
})
factors = [10, 20, 30]
with pf.set_parallel_backend_context("local_multiprocessing"):
result = multiply_by_row(factors, dataframe)
print(result)
# A B
# 0 10 40
# 1 40 100
# 2 90 180
Here we are using two partitioning functions, by_chunk() and by_row().
These split the arguments in to equally sized partitions. It’s semantically equivalent to the following code:
size = min(len(factors), len(dataframe))
for begin in range(0, size, PARTITION_SIZE):
end = min(begin + PARTITION_SIZE, size)
multiply_by_row(factors[begin:end], dataframe.iloc[begin:end])
Sometimes it might be desirable to partition all of the arguments the same way, this can be done with all_arguments():
import pandas as pd
import parfun as pf
@pf.parallel(
split=pf.all_arguments(pf.dataframe.by_group(by=["year", "month"])),
combine_with=pf.dataframe.concat,
)
def monthly_sum(sales: pd.DataFrame, costs: pd.DataFrame) -> pd.DataFrame:
merged = pd.merge(sales, costs, on=["year", "month", "day"], how="outer")
# Group and sum by day
grouped = merged.groupby(["year", "month", "day"], as_index=False).sum(numeric_only=True)
return grouped
if __name__ == "__main__":
sales = pd.DataFrame({
"year": [2024, 2024, 2024],
"month": [1, 1, 2],
"day": [1, 2, 1],
"sales": [100, 200, 150]
})
costs = pd.DataFrame({
"year": [2024, 2024, 2024],
"month": [1, 1, 2],
"day": [1, 2, 1],
"costs": [50, 70, 80]
})
with pf.set_parallel_backend_context("local_multiprocessing"):
result = monthly_sum(sales, costs)
print(result)
# year month day sales costs
# 0 2024 1 1 100 50
# 1 2024 1 2 200 70
# 2 2024 2 1 150 80
Combining functions
In addition to the partitioning function, the @parallel decorator requires a combining function (combine_with) to
collect results and handle the reduction stage of map-reduce.
Parfun provides useful combining functions for handling Python lists
and Pandas dataframes, such as: concat() and concat().
Custom partitioning and combining functions
Parfun has many built-in partitioning and combining functions, but you can also define your own:
from typing import Generator, Iterable, Tuple
import pandas as pd
import parfun as pf
def partition_by_day_of_week(dataframe: pd.DataFrame) -> Generator[Tuple[pd.DataFrame], None, None]:
"""Divides the computation on the "datetime" value, by day of the week (Monday, Tuesday ...)."""
for _, partition in dataframe.groupby(dataframe["datetime"].dt.day_of_week):
yield partition, # Should always yield a tuple that matches the input parameters.
def combine_results(dataframes: Iterable[pd.DataFrame]) -> pd.DataFrame:
"""Collects the results by concatenating them, and make sure the values are kept sorted by date."""
return pd.concat(dataframes).sort_values(by="datetime")
@pf.parallel(
split=pf.all_arguments(partition_by_day_of_week),
combine_with=combine_results,
)
def daily_mean(dataframe: pd.DataFrame) -> pd.DataFrame:
return dataframe.groupby(dataframe["datetime"].dt.date).mean(numeric_only=True)
if __name__ == "__main__":
dataframe = pd.DataFrame({
# Probing times
"datetime": pd.to_datetime([
"2025-04-01 06:00", "2025-04-01 18:00", "2025-04-02 10:00", "2025-04-03 14:00", "2025-04-03 23:00",
"2025-04-04 08:00", "2025-04-05 12:00", "2025-04-06 07:00", "2025-04-06 20:00", "2025-04-07 09:00",
"2025-04-08 15:00", "2025-04-09 11:00", "2025-04-10 13:00", "2025-04-11 06:00", "2025-04-12 16:00",
"2025-04-13 17:00", "2025-04-14 22:00", "2025-04-15 10:00", "2025-04-16 09:00", "2025-04-17 13:00",
"2025-04-18 14:00", "2025-04-19 18:00", "2025-04-20 07:00", "2025-04-21 20:00", "2025-04-22 15:00",
]),
# Temperature values (°C)
"temperature": [
7.2, 10.1, 9.8, 12.5, 11.7,
8.9, 13.0, 7.5, 10.8, 9.3,
12.1, 11.5, 13.3, 6.8, 12.7,
13.5, 9.2, 10.0, 9.9, 11.8,
12.4, 10.6, 7.9, 9.5, 11.6,
],
# Humidity values (%)
"humidity": [
85, 78, 80, 75, 76,
88, 73, 89, 77, 84,
72, 74, 70, 90, 71,
69, 86, 81, 83, 76,
74, 79, 87, 82, 73,
]
})
with pf.set_parallel_backend_context("local_multiprocessing"):
result = daily_mean(dataframe)
print(result)
Partitioning functions are implemented as generators, whereas combining functions accept an iterable of results and return the combined result.
Custom partitioning functions should:
use the
yieldmechanism, and not return a collection (e.g. a list). Returning a collection instead of using a generator will lead to deteriorated performances and higher memory usage.accept the parameters to partition, and yield these partitioned parameters as a tuple, in the same order.
Partition size estimate
Parfun tries to automatically determine the optimal size for the parallelly distributed partitions.
Read more about how the library computes the optimal partition size.
You can override how the library chooses the partition size to use by providing either the
initial_partition_size: int or fixed_partition_size: int parameter:
import numpy as np
import pandas as pd
import parfun as pf
# With `fixed_partition_size`, the input dataframe will always be split in chunks of 1000 rows.
@pf.parallel(
split=pf.all_arguments(pf.dataframe.by_row),
combine_with=sum,
fixed_partition_size=1000,
)
def fixed_partition_size_sum(dataframe: pd.DataFrame) -> float:
return dataframe.values.sum()
# With `initial_partition_size`, the input dataframe will be split in chunks of 1000 rows until Parfun's
# machine-learning algorithm find a better estimate.
@pf.parallel(
split=pf.all_arguments(pf.dataframe.by_row),
combine_with=sum,
initial_partition_size=1000,
)
def initial_partition_size_sum(dataframe: pd.DataFrame) -> float:
return dataframe.values.sum()
# Both `fixed_partition_size` and `initial_partition_size` can accept a callable instead of an integer value. This
# allows for partition sizes to be computed based on the input parameters.
@pf.parallel(
split=pf.all_arguments(pf.dataframe.by_row),
combine_with=sum,
initial_partition_size=lambda dataframe: max(10, len(dataframe) // 4),
)
def computed_partition_size_sum(dataframe: pd.DataFrame) -> float:
return dataframe.values.sum()
if __name__ == "__main__":
dataframe = pd.DataFrame(
np.random.randint(0, 100, size=(100, 3)),
columns=["alpha", "beta", "gamma"],
)
with pf.set_parallel_backend_context("local_multiprocessing"):
print(fixed_partition_size_sum(dataframe))
print(initial_partition_size_sum(dataframe))
print(computed_partition_size_sum(dataframe))
Note
Partition size estimation is disabled for custom partition generators.
Nested parallel function calls
Parfun functions can be safely called from other Parfun functions.
Note
Currently, Scaler is the only backend that can run nested functions in parallel and other backends will execute the functions sequentially.
import pprint
import random
from typing import List
import parfun as pf
@pf.parallel(
split=pf.all_arguments(pf.py_list.by_chunk),
combine_with=pf.py_list.concat,
)
def add_vectors(vec_a: List, vec_b: List) -> List:
"""Add two vectors, element-wise."""
return [a + b for a, b in zip(vec_a, vec_b)]
@pf.parallel(
split=pf.all_arguments(pf.py_list.by_chunk),
combine_with=pf.py_list.concat,
)
def add_matrices(mat_a: List[List], mat_b: List[List]) -> List[List]:
"""Add two matrices, row by row."""
return [add_vectors(vec_a, vec_b) for vec_a, vec_b in zip(mat_a, mat_b)]
if __name__ == "__main__":
N_ROWS, N_COLS = 10, 10
mat_a = [[random.randint(0, 99) for _ in range(0, N_COLS)] for _ in range(0, N_ROWS)]
mat_b = [[random.randint(0, 99) for _ in range(0, N_COLS)] for _ in range(0, N_ROWS)]
print("A =")
pprint.pprint(mat_a)
print("B =")
pprint.pprint(mat_b)
with pf.set_parallel_backend_context("local_multiprocessing"):
result = add_matrices(mat_a, mat_b)
print("A + B =")
pprint.pprint(result)
Profiling
The easiest way to profile the speedup provided by a parallel function is to either use Python’s timeit module, or the
IPython/Jupyter %timeit command.
In addition, the ``@parallel`` decorator accepts a profile: bool and a trace_export: Optional[str] parameter that
can be used get profiling metrics about the execution of a parallel function.
from typing import List
import random
import parfun as pf
@pf.parallel(
split=pf.all_arguments(pf.py_list.by_chunk),
combine_with=sum,
profile=True,
trace_export="parallel_sum_trace.csv",
)
def parallel_sum(values: List) -> List:
return sum(values)
if __name__ == "__main__":
N_VALUES = 100_000
values = [random.randint(0, 99) for _ in range(0, N_VALUES)]
with pf.set_parallel_backend_context("local_multiprocessing"):
print("Sum =", parallel_sum(values))
Setting profile to True returns a performance summary with timings:
parallel_sum()
total CPU execution time: 0:00:00.372508.
compute time: 0:00:00.347168 (93.20%)
min.: 0:00:00.001521
max.: 0:00:00.006217
avg.: 0:00:00.001973
total parallel overhead: 0:00:00.025340 (6.80%)
total partitioning: 0:00:00.024997 (6.71%)
average partitioning: 0:00:00.000142
total combining: 0:00:00.000343 (0.09%)
maximum speedup (theoretical): 14.70x
total partition count: 176
estimator state: running
estimated partition size: 3127
total CPU execution time is the actual CPU time required to execute the parallel function.
This duration is larger than the value returned by
%timeitbecause it sums the execution times for all the cores that processed the function. It also includes the additional processing required to run Parfun (e.g. for partitioning the input and combining the results).compute time is how much CPU time was spent doing the actual computation.
This value should roughly match the duration of the original sequential function if measured with
%timeit. The min, max, and avg values aggregate timing information across the partitioned parallel function calls.total parallel overhead, total partitioning, and total combining are the overheads related to the parallel execution of the function.
These overheads limit the performance gains achievable through parallelization.
maximum speedup (theoretical) estimates how much faster the function would run on a parallel machine with an unlimited number of cores.
This value is calculated based on the input data size, function behavior, and the measured parallel overheads.
total partition count and current estimated partition size describe how Parfun is splitting the input data.
The library uses heuristics to estimate the optimal partition size. The library tries to find a partition size that provides significant parallel speedup without causing too much parallel overhead. Read more about how the optimal partition size is estimated.
Note
As the library is constantly learning the optimal partition size, the first call to the parallelized function might not produce the most optimal timings. In these cases, it is recommended to call the function multiple times before analyzing the profiler output.
When setting the trace_export parameter, Parfun will dump the latest parallel function call metrics to the provided
CSV file. All durations in this file are measured in nanoseconds (10E–9).